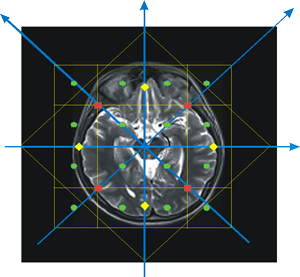
Gradient magnetic field signal phase-frequency coding modification for data regularization in magnetic resonance imaging

Andrii V. Netreba; Oleg A. Naguliak; Andrii O. Komarov

doi:10.3103/S0735272721060017

Authors

Andrii V. Netreba Taras Shevchenko National University of Kyiv, Kyiv, Ukraine
Oleg A. Naguliak Taras Shevchenko National University of Kyiv, Kyiv, Ukraine
Andrii O. Komarov Taras Shevchenko National University of Kyiv, Kyiv, Ukraine

DOI:

https://doi.org/10.3103/S0735272721060017

Keywords:

magnetic resonance imaging, MRI, nuclear magnetic resonance, NMR, gradient K-space of magnetic field, reconstruction, superresolution

Abstract

The reconstruction of tomograms in magnetic resonance imaging (MRI) has been considered for different degrees of transverse gradient instability of magnetic field. A method for minimizing the impact of deviation of resultant points of signal measurements from regular positions on the quality of reconstructed tomograms was proposed. The ultimate values of parameters of field gradient instability with due regard for the possibility of their compensation were determined in processing of real tomographic images. A series of multiple procedures for generating signals under conditions of different spread of magnetic field components and subsequent reconstruction was conducted for estimating the impact of instability on the accuracy of final results. It has been shown that the building and joint analysis of several tomographic distributions for different angles of orientation of magnetic gradient system for the transverse phase-frequency coding of response signal improves the structure of diagnostic data. In solving the inverse problem of restoring the spin distributions, the compensation of distortions caused by the irregularity of grid for forming data through combining an array of measurements performed under different conditions was obtained. The estimation of qualitative parameters of reconstruction of two-dimensional tomographic high-resolution distributions was conducted for the case of measuring the response signal for two and three orientations of its transverse coding.

References

O. O. Naguliak, A. V. Netreba, “The influence of the time MR sequence parameters on the diffusion weighted imaging sensitivity,” J. Phys. Stud., vol. 19, no. 1/2, p. 1002, 2015, doi: https://doi.org/10.30970/jps.19.1002.

S. P. M. Crijns, B. W. Raaymakers, J. J. W. Lagendijk, “Real-time correction of magnetic field inhomogeneity-induced image distortions for MRI-guided conventional and proton radiotherapy,” Phys. Med. Biol., vol. 56, no. 1, pp. 289–297, 2011, doi: https://doi.org/10.1088/0031-9155/56/1/017.

M. Espy et al., “Ultra-low-field MRI for the detection of liquid explosives,” Supercond. Sci. Technol., vol. 23, no. 3, p. 034023, 2010, doi: https://doi.org/10.1088/0953-2048/23/3/034023.

R. Ladebeck, D. Martin, S. Schmidt, “Mobile comb. MRI/PET app.,” US Patent US20090043189, 2009.

M. V. Kononov, O. A. Nagulyak, A. V. Netreba, “Influence of X-radiation in receiver system on reconstruction performance of projection tomography,” Radioelectron. Commun. Syst., vol. 51, no. 3, pp. 163–165, 2008, doi: https://doi.org/10.3103/S0735272708030084.

O. O. Naguliak, A. V. Netreba, S. P. Radchenko, O. O. Sudakov, “Increasing of the MR imaging spatial resolution by data estimation in k-space,” in 2017 IEEE 37th International Conference on Electronics and Nanotechnology (ELNANO), 2017, pp. 310–315, doi: https://doi.org/10.1109/ELNANO.2017.7939769.

E. Plenge et al., “Super-resolution methods in MRI: Can they improve the trade-off between resolution, signal-to-noise ratio, and acquisition time?,” Magn. Reson. Med., vol. 68, no. 6, pp. 1983–1993, 2012, doi: https://doi.org/10.1002/mrm.24187.

A. V. Netreba, A. O. Komarov, “Influence of the transverse gradient magnetic fields instability to reconstruction in MR imaging,” in 2017 IEEE International Young Scientists Forum on Applied Physics and Engineering (YSF), 2017, pp. 139–142, doi: https://doi.org/10.1109/YSF.2017.8126660.

A. Rueda, N. Malpica, E. Romero, “Single-image super-resolution of brain MR images using overcomplete dictionaries,” Med. Image Anal., vol. 17, no. 1, pp. 113–132, 2013, doi: https://doi.org/10.1016/j.media.2012.09.003.

E. Van Reeth, I. W. K. Tham, C. H. Tan, C. L. Poh, “Super-resolution in magnetic resonance imaging: A review,” Concepts Magn. Reson. Part A, vol. 40A, no. 6, pp. 306–325, 2012, doi: https://doi.org/10.1002/cmr.a.21249.

A. V. Akimov, A. A. Sirota, “Synthesis and analysis of algorithms for digital signal recognition in conditions of deforming distortions and additive noise,” Radioelectron. Commun. Syst., vol. 60, no. 10, pp. 458–468, 2017, doi: https://doi.org/10.3103/S0735272717100041.

E. D. Prilepsky, J. E. Prilepsky, “Estimation of optimal parameter of regularization of signal recovery,” Radioelectron. Commun. Syst., vol. 61, no. 9, pp. 406–418, 2018, doi: https://doi.org/10.3103/S0735272718090030.

D. Y. Golovanov, V. I. Parfenov, “Detection efficiency of signal with unknown non-power parameter using algorithms based on the compressive sensing theory,” Radioelectron. Commun. Syst., vol. 61, no. 8, pp. 361–370, 2018, doi: https://doi.org/10.3103/S0735272718080046.

P. Y. Kostenko, V. V. Slobodyanuk, A. N. Barsukov, “Stealthiness of analytical chaotic signals,” Radioelectron. Commun. Syst., vol. 60, no. 3, pp. 132–140, 2017, doi: https://doi.org/10.3103/S0735272717030050.

V. V. Savchenko, “Criterion for minimum of mean information deviation for distinguishing random signals with similar characteristics,” Radioelectron. Commun. Syst., vol. 61, no. 9, pp. 419–430, 2018, doi: https://doi.org/10.3103/S0735272718090042.

N. G. Ivanushkina et al., “Analysis of electrocardiosignals for formation of the diagnostic features of post-traumatic myocardial dystrophy,” Radioelectron. Commun. Syst., vol. 60, no. 9, pp. 521–530, 2017, doi: https://doi.org/10.3103/S0735272717090047.

S. M. Vovk, V. F. Borulko, “Determination of amplitude levels of the piecewise constant signal by using polynomial approximation,” Radioelectron. Commun. Syst., vol. 60, no. 3, pp. 113–122, 2017, doi: https://doi.org/10.3103/S0735272717030037.

A. A. Kolchev, A. E. Nedopekin, “Application of model of mixture of probabilistic distributions for definition of the signals of radiophysical probing,” Radioelectron. Commun. Syst., vol. 59, no. 8, pp. 362–368, 2016, doi: https://doi.org/10.3103/S0735272716080057.

E. V. Storchun, E. I. Yakovenko, “Performance analysis of the recording system of nonlocal biomechanical signals,” Radioelectron. Commun. Syst., vol. 59, no. 8, pp. 375–378, 2016, doi: https://doi.org/10.3103/S0735272716080070.

V. I. Naidenko, “Uniform isotropic medium excitation with magnetic field step,” Radioelectron. Commun. Syst., vol. 59, no. 6, pp. 274–279, 2016, doi: https://doi.org/10.3103/S0735272716060078.

A. I. Rybin, A. D. Melnyk, Y. K. Nizhebetskaya, I. A. Sushko, S. N. Litvintsev, “Pattern recognition of 1D and 2D signals using normalization and normal transformation,” Radioelectron. Commun. Syst., vol. 59, no. 1, pp. 28–38, 2016, doi: https://doi.org/10.3103/S0735272716010027.

V. S. Korolyuk, N. I. Portenko, A. V. Skorokhod, A. F. Turbin, Handbook of Probability Theory and Mathematical Statistics, [in Russian]. Moscow: Nauka, 1985.

C. Debus, R. Floca, D. Nörenberg, A. Abdollahi, M. Ingrisch, “Impact of fitting algorithms on errors of parameter estimates in dynamic contrast-enhanced MRI,” Phys. Med. Biol., vol. 62, no. 24, pp. 9322–9340, 2017, doi: https://doi.org/10.1088/1361-6560/aa8989.

A. O. Komarov, O. O. Naguliak, A. V. Netreba, S. P. Radchenko, O. O. Sudakov, “Compensation of the magnetic gradient instability in MRI by measurements data for several angular orientations,” in 2018 IEEE 38th International Conference on Electronics and Nanotechnology (ELNANO), 2018, pp. 355–359, doi: https://doi.org/10.1109/ELNANO.2018.8477435.

D. I. Lekhovytskiy, “Adaptive lattice filters for systems of space-time processing of non-stationary Gaussian processes,” Radioelectron. Commun. Syst., vol. 61, no. 11, pp. 477–514, 2018, doi: https://doi.org/10.3103/S0735272718110018.

A. A. Borodyn, “Method of images segmentation by dynamic spectral characteristics,” Radioelectron. Commun. Syst., vol. 59, no. 1, pp. 47–51, 2016, doi: https://doi.org/10.3103/S0735272716010040.