Simple technique for biconical cavity eigenfrequency determination
DOI:
https://doi.org/10.3103/S0735272717120056Keywords:
biconical cavity, collocation method, dispersion equation, eigenfrequency, overlapping domain decomposition methodAbstract
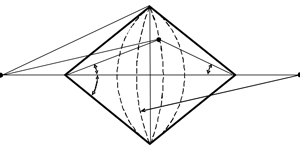
A number of features of biconical cavities make them attractive for various applications. Expressions for the calculation of the eigenfrequencies of a biconical cavity with large cone angles can be derived using the overlapping domain decomposition method in combination with the collocation method; however, the expressions reported in the literature involve only a single pair of collocation points, thus giving no way to estimate the eigenfrequency determination accuracy. The aim of this paper is to calculate the biconical cavity eigenfrequencies for an arbitrary number of collocation point pairs. An equation in the biconical cavity eigenfrequencies for an azimuthally symmetric transverse electric field at an arbitrary number of collocation point pairs is derived. The equation reduces to two equations, whose solution requires far less computational effort in comparison with the original equation. The solution of one of the two equations are based on modes symmetric about the cavity symmetry plane, and the solutions of the other are based on antisymmetric modes. The calculated eigenfrequencies converge rapidly with increasing number of collocation point pairs, while the use of only one collocation point pair may introduce noticeable error. The proposed technique may be used in the development of components and units on the basis of biconical cavities.References
- EGOROV, V.N. Resonance methods for microwave studies of dielectrics (Review). Instrum. Exp. Tech., v.50, n.2, p.143-175, 2007. DOI: https://doi.org/10.1134/S0020441207020017.
- AFSAR, M.N.; BIRCH, J.R.; CLARKE, R.N.; Chantry, G.W. The measurement of the properties of materials. Proc. IEEE, v.74, n.1, p.183-199, 1986. DOI: https://doi.org/10.1109/PROC.1986.13432.
- BUSSEY, H.E.; MORRIS, D.; ZAL’TSMAN, E.B. International comparison of complex permittivity measurement at 9 GHz. IEEE Trans. Instrum. Meas., v.23, n.3, p.235-239, 1974. DOI: https://doi.org/10.1109/TIM.1974.4314270.
- NI, E.; STUMPER, U. Permittivity measurements using a frequency-tuned microwave TE01 cavity resonator. IEE Proc. H - Microwaves, Antennas and Propagation, v.132, n.1, p.27-32, 1985. DOI: https://doi.org/10.1049/ip-h-2:19850005.
- KLING, C.K.; WHITES, K.W.; GROVEN, L.J. Accurate specimen placement for dielectric measurements in TM0n0 cylindrical cavity. Proc. of IEEE Int. Symp. on Antennas and Propagation, APSURSI, 26 June-1 July 2016, Fajardo, Puerto Rico. IEEE, 2016, p.1995-1996. DOI: https://doi.org/10.1109/APS.2016.7696704.
- SYDORUK, V.A.; FIORANI, F.; JAHNKE, S.; KRAUSE, H.-J. Design and characterization of microwave cavity resonators for noninvasive monitoring of plant water distribution. IEEE Trans. Microwave Theory Tech., v.64, n.9, p.2894-2904, 2016. DOI: https://doi.org/10.1109/TMTT.2016.2594218.
- DROBAKHIN, O.O.; ZABOLOTNYY, P.I.; PRIVALOV, Y.N. Taking into account the impact of coupling elements on the resonance phenomena in biconical resonators. Radioelectron. Commun. Syst., v.53, n.7, p.389-394, 2010. DOI: https://doi.org/10.3103/S0735272710070071.
- DROBAKHIN, O.O.; PRIVALOV, Y.N.; SALTYKOV, D.Y. Open-ended waveguide cutoff resonators for monitoring dielectrics parameters of gases. Telecommun. Radio Eng., v.72, n.7, p.627-640, 2013. DOI: http://doi.org/10.1615/TelecomRadEng.v72.i7.60.
- ANDREEV, M.V.; DROBAKHIN, O.O.; PRIVALOV, Y.N.; SALTYKOV, D.Y. Measurement of dielectric material properties using coupled biconical resonators. Telecommun. Radio Eng., v.73, n.11, p.1017-1032, 2014. DOI: http://doi.org/10.1615/TelecomRadEng.v73.i11.70.
- ALIMOV, A.A.; RADIONOV, A.A. The open limit biconical resonator calculation. Antennas, n.4, p.40-45, 2015. URI: https://elibrary.ru/item.asp?id=23366163.
- VAN’T HOF, J.P.; STANCIL, D.D. Eigenfrequencies of a truncated conical resonator via the classical and Wentzel–Kramers–Brillouin methods. IEEE Trans. Microwave Theory Tech., v.56, n.8, p.1909-1916, 2008. DOI: https://doi.org/10.1109/TMTT.2008.927408.
- KURYLIAK, D.B.; NAZARCHUK, Z.T.; TRISHCHUK, O.B. Axially-symmetric TM-waves diffraction by sphere-conical cavity. PIER B, v.73, p.1-16, 2017. DOI: http://dx.doi.org/10.2528/PIERB16120904.
- HOPPE, R.H.W.; KUZNETSOV, Y.A. Overlapping domain decomposition methods with distributed Lagrange multipliers. J. Numerical Math., v.9, n.1, p.285-293, 2001.
- DROBAKHIN, O.O.; ZABOLOTNYY, P.I.; PRIVALOV, Y.N. Approximate calculation of eigenfrequencies of biconical microwave cavities. Radioelectron. Commun. Syst., v.56, n.3, p.127-132, 2013. DOI: https://doi.org/10.3103/S0735272713030035.
Downloads
Published
2017-12-23
Issue
Section
Research Articles

