Effective high-precision analysis of thin asymmetric inductive diaphragm in rectangular waveguide using integral equation method
DOI:
https://doi.org/10.3103/S0735272721020035Keywords:
mathematical model, infinitely thin asymmetric inductive diaphragm, singularity of tangential electric field at ridge, rectangular waveguide, Gegenbauer polynomials, generalized scattering matrixAbstract
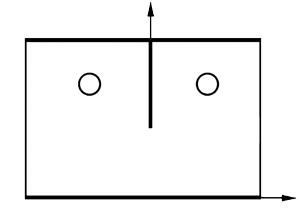
This paper proposes a solution of the electrodynamic problem of determining the generalized scattering matrix of infinitely thin asymmetric one-sided inductive diaphragm in rectangular waveguide using the integral equation method. The problem is reduced to solving the system of integral equations in terms of the number of incident modes falling on the inhomogeneity from the left partial region. The efficiency of the new solution of electrodynamic problem is achieved owing to the correct way of taking into account the singularity of tangential electric field in the diaphragm aperture using the Gegenbauer polynomials. The Galerkin method is used to reduce each integral equation to the system of linear algebraic equations in complex coefficients of the expansion of tangential electric field in the diaphragm window. Numerical investigation of the obtained solution was conducted for determining the equivalent parameters of diaphragm in the frequency band where only the principal mode can propagate along the waveguide without attenuation. The possibility of effective high-accuracy calculation of the generalized scattering matrix of infinitely thin asymmetric inductive diaphragm in rectangular waveguide with due regard for singularity of tangential electric field at the sharp ridge in the diaphragm window has been confirmed.
References
- O. O. Drobakhin, S. V. Plaksin, V. D. Ryabchii, D. Y. Saltykov, Microwave Technology and Semiconductor Electronics, [in Russian]. Sevastopol: Veber, 2013.
- V. A. Neganov, D. P. Klyuev, D. P. Tabakov, “Part 1: Designing, Implementation, and Examples of Microwave Device Applications,” in Microwave Devices and Antennas, Moscow: Librokom, 2013.
- J. A. Ruiz-Cruz, J. R. Montejo-Garai, J. M. Rebollar, “Computer aided design of waveguide devices by mode-matching methods,” in Passive Microwave Components and Antennas, V. Zhurbenko, Ed. Vuko-var: InTech, 2010.
- Y. D. Chernousov, V. I. Ivannikov, I. V. Shebolaev, A. E. Levichev, V. M. Pavlov, “Bandpass characteristics of coupled resonators,” J. Commun. Technol. Electron., vol. 55, no. 8, pp. 863–869, 2010, doi: https://doi.org/10.1134/S1064226910080036.
- S. Choocadee, S. Akatimagool, “The simulation, design and implementation of bandpass filters in rectangular waveguides,” Electr. Electron. Eng., vol. 2, no. 3, pp. 152–157, 2012, doi: https://doi.org/10.5923/j.eee.20120203.08.
- Y. D. Chernousov, A. E. Levichev, V. M. Pavlov, G. K. Shamuilov, “Thin diaphragm in the rectangular waveguide,” Vestn. NGU. Seriya Fiz., vol. 6, no. 1, pp. 44–49, 2011.
- M. V. Mishchenko, A. Y. Farafonov, D. A. Kovalenko, Y. A. Sitsilitsin, “Synthesis method of tolerance deviations to the geometrical parameter of the microstrip devices,” Radio Electron. Comput. Sci. Control, no. 2, pp. 21–27, 2014, doi: https://doi.org/10.15588/1607-3274-2013-2-3.
- H. Yan, X. Wu, J. Yang, “Application of Monte Carlo method in tolerance analysis,” Procedia CIRP, vol. 27, pp. 281–285, 2015, doi: https://doi.org/10.1016/j.procir.2015.04.079.
- G. F. Zargano, A. M. Lerer, V. P. Lyapin, G. P. Sinyavskii, Transmission Lines with Complex Cross Sections, [in Russian]. Rostov: Izd. Rostovskogo Universiteta, 1983.
- D. B. Mamedov, A. G. Yushchenko, “Research of scattering matrix method convergence in the computation problem of quasi-h mode microwave filters,” Eastern-European J. Enterp. Technol., vol. 4, no. 9(76), p. 34, 2015, doi: https://doi.org/10.15587/1729-4061.2015.47992.
- O. S. Zakharchenko, S. Y. Martynyuk, P. Y. Stepanenko, “Generalized mathematical model of thin asymmetric inductive diaphragm in rectangular waveguide,” Visnyk NTUU KPI Seriia - Radiotekhnika Radioaparatobuduvannia, no. 72, pp. 13–22, 2018, doi: https://doi.org/10.20535/RADAP.2018.72.13-22.
- S. O. Steshenko, S. A. Prikolotin, A. A. Kirilenko, D. Y. Kulik, L. A. Rud’, S. L. Senkevich, “Partial domain technique considering field singularities in the internal problems with arbitrary piecewise-coordinate boundaries: Part 2. Plane-transverse junctions and ‘in-line’ objects,” Telecommun. Radio Eng., vol. 73, no. 3, pp. 187–201, 2014, doi: https://doi.org/10.1615/TelecomRadEng.v73.i3.10.
- V. V. Nikolskii, T. I. Nikolskaya, Electrodynamics and Wave Propagation, [in Russian]. Moscow: Librokom, 2015.
- V. F. Kravchenko, O. S. Labunko, A. M. Lerer, G. P. Sinyavskii, Computational Methods in Modern Radiophysics, [in Russian]. Moscow: Fizmatlit, 2009.
- I. S. Gradstein, I. M. Ryzhik, Tables of Integrals, Series and Products, [in Russian]. St. Petersburg: BKhV-Peterburg, 2011.
- N. S. Bakhvalov, N. P. Zhidkov, G. M. Kobelkov, Numerical Methods, [in Russian]. Moscow: Binom, 2008.
- F. F. Dubrovka, Y. A. Ovsianyk, P. Y. Stepanenko, O. S. Zakharchenko, “Wideband matching the dual frequency coaxial waveguide feed,” Inf. Telecommun. Sci., vol. 3, no. 2, pp. 53–60, 2012, uri: http://infotelesc.kpi.ua/article/view/30217.
- F. F. Dubrovka, S. I. Piltyay, “Eigenmodes of sectoral coaxial ridged waveguides,” Radioelectron. Commun. Syst., vol. 55, no. 6, pp. 239–247, 2012, doi: https://doi.org/10.3103/S0735272712060015.
- F. F. Dubrovka, S. I. Piltyay, “Electrodynamics boundary problem solution for sectoral coaxial ridged waveguides by integral equation technique,” Radioelectron. Commun. Syst., vol. 55, no. 5, pp. 191–203, 2012, doi: https://doi.org/10.3103/S0735272712050019.
- F. F. Dubrovka, S. I. Piltyay, “Eigenmodes of coaxial quad-ridged waveguides. Theory,” Radioelectron. Commun. Syst., vol. 57, no. 1, pp. 1–30, 2014, doi: https://doi.org/10.3103/S0735272714010014.