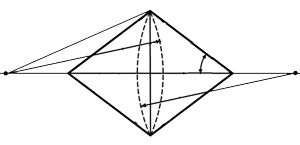
Simple technique for determining length of biconical cavity’s evanescent zones

Mikhail Andreev; Oleg Drobakhin; Nikolai Gorev; I. F. Kodzhespirova; Dmitry Saltykov

doi:10.3103/S0735272724010011

Authors

Mikhail Andreev Oles Honchar Dnipro National University, Dnipro, Ukraine https://orcid.org/0000-0001-7360-8058
Oleg Drobakhin Oles Honchar Dnipro National University, Dnipro, Ukraine https://orcid.org/0000-0003-2624-9122
Nikolai Gorev Institute of Technical Mechanics of National Academy of Sciences of Ukraine and State Space Agency of Ukraine, Dnipro, Ukraine https://orcid.org/0000-0001-6739-5172
I. F. Kodzhespirova Institute of Technical Mechanics of National Academy of Sciences of Ukraine and State Space Agency of Ukraine, Dnipro, Ukraine https://orcid.org/0000-0001-8975-712X
Dmitry Saltykov Oles Honchar Dnipro National University, Dnipro, Ukraine https://orcid.org/0000-0001-5403-4773

DOI:

https://doi.org/10.3103/S0735272724010011

Keywords:

biconical cavity, collocation method, eigenfunction expansion, evanescent zone, overlapping domain decomposition

Abstract

This paper presents a simple technique for finding the length of evanescent zones near the ends of the biconical cavity, where sample insertion openings can be made without significantly affecting the resonance frequencies or the field structure. The technique combines the overlapping domain decomposition method with the collocation method. The interior of the cavity is divided into two overlapping regions, on the boundaries of which collocation points are specified. In each region, the electric field is represented as an eigenfunction expansion. A homogeneous system of linear equations in the expansion coefficients is derived from the equality of the electric fields in both regions at the collocation points. The expansion coefficients are determined as an eigenvector of the system matrix associated with its zero eigenvalue. Using the found expansion coefficients, the distribution of the electric field normalized to the maximum electric field in the cavity is calculated to give the length of evanescent zones, which are defined as regions where the electric field does not exceed a specified small fraction of the maximum electric field in the cavity. Because as few as four pairs of collocation points were proved to be sufficient, the computational effort of the proposed technique is relatively moderate, thus allowing it to be used in the development of instruments based on open-ended biconical cavities.

References

R. I. Bilous, A. P. Motornenko, “Comparison of characteristics of resonator on the basis of evanescent waveguides in millimeter wavelength band,” Telecommun. Radio Eng., vol. 66, no. 15, pp. 1365–1369, 2007, doi: https://doi.org/10.1615/TelecomRadEng.v66.i15.30.

S. M. Jensen, R. B. Bass, A. W. Lichtenberger, A. M. Datesman, “A simple GHz resonator for superconducting materials characterization,” IEEE Trans. Appl. Supercond., vol. 25, no. 3, pp. 1–4, 2015, doi: https://doi.org/10.1109/TASC.2014.2379285.

A. Rashidian, L. Shafai, D. Klymyshyn, C. Shafai, “A fast and efficient free-space dielectric measurement technique at mm-wave frequencies,” IEEE Antennas Wirel. Propag. Lett., vol. 16, pp. 2630–2633, 2017, doi: https://doi.org/10.1109/LAWP.2017.2737632.

M. V. Andreev, O. O. Drobakhin, Y. N. Privalov, D. Y. Saltykov, “Measurement of dielectric material properties using coupled biconical resonators,” Telecommun. Radio Eng., vol. 73, no. 11, pp. 1017–1032, 2014, doi: https://doi.org/10.1615/TelecomRadEng.v73.i11.70.

O. O. Drobakhin, P. I. Zabolotnyy, Y. N. Privalov, “Taking into account the impact of coupling elements on the resonance phenomena in biconical resonators,” Radioelectron. Commun. Syst., vol. 53, no. 7, pp. 389–394, 2010, doi: https://doi.org/10.3103/S0735272710070071.

O. O. Drobakhin, Y. N. Privalov, D. Y. Saltykov, “Open-ended waveguide cutoff resonators for monitoring dielectrics parameters of gases,” Telecommun. Radio Eng., vol. 72, no. 7, pp. 627–640, 2013, doi: https://doi.org/10.1615/TelecomRadEng.v72.i7.60.

P. Zabolotnyi, “Open-ended microwave biconical cavity for the determination of the average electron density in a low-temperature plasma,” in 2022 IEEE 2nd Ukrainian Microwave Week (UkrMW), 2022, pp. 131–134, doi: https://doi.org/10.1109/UkrMW58013.2022.10037160.

B. Z. Katsenelenbaum, L. Mercader del Rio, M. Pereyaslavets, M. Sorolla Ayza, M. Thumm, Theory of Nonuniform Waveguides: The Cross-Section Method. London: IET, 1998, doi: https://doi.org/10.1049/PBEW044E.

J. P. Van’t Hof, D. D. Stancil, “Eigenfrequencies of a truncated conical resonator via the classical and Wentzel–Kramers–Brillouin methods,” IEEE Trans. Microw. Theory Tech., vol. 56, no. 8, pp. 1909–1916, 2008, doi: https://doi.org/10.1109/TMTT.2008.927408.

P. Zabolotnyy, “On the study of the resonant properties of a biconical cavity with a dielectric rod using the quasiregular approximation method,” in 2014 International Conference on Mathematical Methods in Electromagnetic Theory, 2014, pp. 172–175, doi: https://doi.org/10.1109/MMET.2014.6928759.

K. G. Savin, I. P. Golubeva, Y. V. Prokopenko, “Calculation of frequency and power characteristics of the composite metal-dielectric resonator using the method of partial regions,” Radioelectron. Commun. Syst., vol. 59, no. 5, pp. 229–236, 2016, doi: https://doi.org/10.3103/S0735272716050058.

D. B. Kuryliak, Z. T. Nazarchuk, O. B. Trishchuk, “Axially-symmetric TM-waves diffraction by sphere-conical cavity,” Prog. Electromagn. Res. B, vol. 73, pp. 1–16, 2017, doi: https://doi.org/10.2528/PIERB16120904.

O. O. Drobakhin, P. I. Zabolotnyy, Y. N. Privalov, “Approximate calculation of eigenfrequencies of biconical microwave cavities,” Radioelectron. Commun. Syst., vol. 56, no. 3, pp. 127–132, 2013, doi: https://doi.org/10.3103/S0735272713030035.

S. A. Kostylev, E. F. Prokhorov, N. B. Gorev, I. F. Kodzhespirova, Y. A. Kovalenko, “Low-frequency capacitance–voltage characterization of deep levels in film–buffer layer–substrate GaAs structures,” Solid-State Electron., vol. 43, no. 1, pp. 169–176, 1999, doi: https://doi.org/10.1016/S0038-1101(98)00189-0.

R. H. W. Hoppe, Y. A. Kuznetsov, “Overlapping domain decomposition methods with distributed Lagrange multipliers,” J. Numer. Math., vol. 9, no. 4, 2001, doi: https://doi.org/10.1515/JNMA.2001.285.

M. V. Andreev, O. O. Drobakhin, D. Y. Saltykov, N. B. Gorev, I. F. Kodzhespirova, “Simple technique for biconical cavity eigenfrequency determination,” Radioelectron. Commun. Syst., vol. 60, no. 12, pp. 555–561, 2017, doi: https://doi.org/10.3103/S0735272717120056.

M. V. Andreev, O. O. Drobakhin, D. Y. Saltykov, N. B. Gorev, I. F. Kodzhespirova, “Determination of biconical cavity eigenfrequencies using method of partial intersecting regions and approximation by rational fractions,” Radioelectron. Commun. Syst., vol. 62, no. 12, pp. 630–641, 2019, doi: https://doi.org/10.3103/S0735272719120033.

O. O. Drobakhin, “Prony’s-method identification of parameters of model which is sum of exponential functions,” Optoelectron. Instrumentation, Data Process., no. 4, pp. 37–42, 1989.

T. K. Sarkar, M. Salazar-Palma, M. Da Zhu, H. Chen, Modern Characterization of Electromagnetic Systems and Its Associated Metrology. Wiley-IEEE Press, 2021.