Refinement of expression for calculating losses of single-layer winding of inductive element

Andrii Seredin; Andrii Movchaniuk; Oksana Zakharchenko; Nikita Yezerskyi

doi:10.3103/S0735272723120038

Authors

Andrii Seredin National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Kyiv, Ukraine https://orcid.org/0000-0002-4919-4614
Andrii Movchaniuk National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Kyiv, Ukraine https://orcid.org/0000-0003-2901-0424
Oksana Zakharchenko National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Kyiv, Ukraine https://orcid.org/0000-0001-6259-5888
Nikita Yezerskyi National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Kyiv, Ukraine https://orcid.org/0000-0002-7482-0832

DOI:

https://doi.org/10.3103/S0735272723120038

Keywords:

ultrasonic frequency range, matching filter, choke, single-layer winding, FEA, finite-element analysis, proximity effect, proximity self-effect, interturn proximity effect, loss resistance, approximation

Abstract

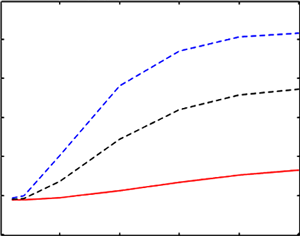
The paper briefly presents the results of preliminary studies, during which it was determined that the probable reason for the appearance of a significant error in calculating the losses of a single-layer winding of inductive element without a core by using the Ferreira analytical technique in the ultrasonic frequency range is the neglect of the influence of some geometric parameters of the winding, such as its diameter and the number of turns, on the current distribution in the turns. Thus, the calculation expression of this technique needs to be refined by including the neglected geometric parameters in this expression. It has been determined that solving the refinement problem analytically is difficult. Therefore, we propose to solve it empirically. Using computer simulation, the losses of a single-layer winding without a core were determined for the most common in-practice values of winding diameters, conductor diameters, the number of turns, and the operating frequencies. Several graphs of relationships are presented, based on which the types of refining expressions and the method of their introduction into the calculation expression as complementary factors are determined; in addition, the corresponding correction factors are calculated. The results of calculating the values of losses by the refined expression and the initial one are compared. It has been established that the discrepancy between the theoretical and experimental results changed from 59.5 to 11% when the number of turns was changed and from 63 to 4% when the influence of the winding diameter was considered.

An alternative method for calculating the value of losses of single-layer windings for most common specific practical cases was proposed. Based on the simulated data, curves of the relationships of the winding losses as a function of the specified geometric parameters were built. The optimal type of approximating function was selected, the approximation was performed, and the approximating coefficients for the conductor diameter, frame diameter, and the number of turns in the winding for different operating frequencies were calculated.

References

H. Choi, “Pre-matching circuit for high-frequency ultrasound transducers,” Sensors, vol. 22, no. 22, p. 8861, 2022, doi: https://doi.org/10.3390/s22228861.

G. Bocock, Essential Guide to Power Supplies. [no info]: XP Power, 2014.

P. L. Dowell, “Effects of eddy currents in transformer windings,” Proc. Inst. Electr. Eng., vol. 113, no. 8, p. 1387, 1966, doi: https://doi.org/10.1049/piee.1966.0236.

J. A. Ferreira, “Improved analytical modeling of conductive losses in magnetic components,” IEEE Trans. Power Electron., vol. 9, no. 1, pp. 127–131, 1994, doi: https://doi.org/10.1109/63.285503.

А. P. Seredin, А. V. Movchaniuk, “Analysis of techniques and modification of existing expressions for calculating choke loss resistance at ultrasonic frequencies,” in Proc. of Int. Sci. Tech. Conf. on Radio Fields, Signals, Apparatus and Systems, 2020, pp. 52–55.

А. P. Seredin, А. V. Movchaniuk, “Influence of the number of turns of the single-layer winding of the inductive element on the resistance of losses,” Visnyk Vinnytsia Politech. Inst., vol. 169, no. 4, pp. 25–32, 2023, doi: https://doi.org/10.31649/1997-9266-2023-169-4-25-32.

A. P. Seredin, A. V. Movchaniuk, “Influence of single layer winding geometry of inductive element on loss resistance,” Radioelectron. Commun. Syst., vol. 65, no. 10, pp. 551–561, 2022, doi: https://doi.org/10.3103/S073527272301003X.

A. P. Seredin, “Refinement of the technique for estimating losses in chokes with single-layer winding,” Kyiv, 2023.

M. Wolf, D. Shmilovitz, “Substantial reduction of solenoidal ferrite rod coil losses through winding geometry modification,” IEEE Trans. Magn., vol. 60, no. 9, pp. 1–5, 2024, doi: https://doi.org/10.1109/TMAG.2024.3422824.

J. R. Gonzalez-Teodoro, V. Kindl, M. Frivaldsky, “Different eddy current effects study for circular windings based on finite elements,” in 2021 25th International Conference Electronics, 2021, pp. 1–6, doi: https://doi.org/10.1109/IEEECONF52705.2021.9467469.

M. Kazimierczuk, High‐Frequency Magnetic Components. Wiley, 2013, doi: https://doi.org/10.1002/9781118717806.

L. Chen, R. Wu, “Empirical analytical inductance calculation and inductance to DC resistance ratio optimization of on-chip solenoid magnetic-core inductors,” in 2022 IEEE 16th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), 2022, pp. 1–3, doi: https://doi.org/10.1109/ICSICT55466.2022.9963436.

The MathWorks, “Curve Fitting Toolbox: For use with MatLAB,” User’s guide. Version 1. http://cda.psych.uiuc.edu/matlab_pdf/curvefit.pdf.