Complex spline approximation in positioning problems
DOI:
https://doi.org/10.3103/S0735272722100028Keywords:
Fingerprinting methodAbstract
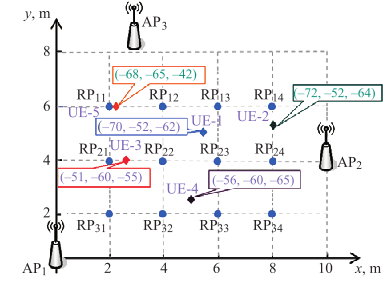
The rapid development of various applications and services that use the user’s current LBS location and crowdsourcing require constant improvement of positioning methods in order to improve location accuracy. The problems of local positioning of users indoors in conditions of high concentration of users and the presence of difficulties in the propagation of radio signals deserve special attention. Comparative analysis of known IPS local positioning methods proves the advantage of using the fingerprinting method according to the criterion of positioning accuracy. It is proposed a method of user positioning in a Wi-Fi/Indoor network, which is based on the fingerprinting method and complex spline approximation. We carry out a comparison of the results of positioning in the Wi-Fi/Indoor network based on the fingerprinting method using different methods of user location determination, such as the k-nearest neighbors k-NN method, the weighted k-nearest neighbors k-WNN method and the complex spline approximation based on the quadratic planar spline. It is shown that application of complex spline approximation provides an increase in the accuracy of user positioning in the Wi-Fi/Indoor network, thereby making it possible to provide LBS-oriented services to users indoors.
References
- M. Y. Ilchenko, L. A. Uryvsky, A. V. Moshinskaya, “Developing telecommunication strategies based on scenarios in the information community,” Cybern. Syst. Anal., vol. 53, no. 6, pp. 905–913, 2017, doi: https://doi.org/10.1007/s10559-017-9992-9.
- M. Ilchenko, L. Uryvsky, S. Osypchuk, “World trends of modern information and telecommunication technologies development,” in 2019 International Conference on Information and Telecommunication Technologies and Radio Electronics (UkrMiCo), 2019, pp. 1–7, doi: https://doi.org/10.1109/UkrMiCo47782.2019.9165461.
- V. Kondratiuk, V. Konin, O. Kutsenko, S. Ilnytska, “Testing static and kinematic modes of precise point positioning service in Ukraine,” Radioelectron. Commun. Syst., vol. 62, no. 10, pp. 530–540, 2019, doi: https://doi.org/10.3103/S0735272719100054.
- S. Y. Zhuk, I. O. Tovkach, Y. Y. Reutska, “Adaptive filtration of radio source movement parameters based on sensor network TDOA measurements in presence of anomalous measurements,” Radioelectron. Commun. Syst., vol. 62, no. 2, pp. 61–71, 2019, doi: https://doi.org/10.3103/S073527271902002X.
- I. O. Tovkach, S. Y. Zhuk, “Adaptive filtration of radio source movement parameters with complex use of sensor network data based on TDOA and RSS methods,” Radioelectron. Commun. Syst., vol. 60, no. 12, pp. 528–537, 2017, doi: https://doi.org/10.3103/S0735272717120020.
- G. Li, E. Geng, Z. Ye, Y. Xu, H. Zhu, “An indoor positioning algorithm based on RSSI real-time correction,” in 2018 14th IEEE International Conference on Signal Processing (ICSP), 2018, pp. 129–133, doi: https://doi.org/10.1109/ICSP.2018.8652382.
- A. P. Rahmadini, P. Kristalina, A. Sudarsono, “Optimization of Fingerprint indoor localization system for multiple object tracking based on iterated weighting constant - KNN method,” Int. J. Adv. Sci. Eng. Inf. Technol., vol. 8, no. 3, p. 998, 2018, doi: https://doi.org/10.18517/ijaseit.8.3.6086.
- B. H. O. U. V. Pinto, H. A. B. F. de Oliveira, E. J. P. Souto, “Factor optimization for the design of indoor positioning systems using a probability-based algorithm,” J. Sens. Actuator Networks, vol. 10, no. 1, p. 16, 2021, doi: https://doi.org/10.3390/jsan10010016.
- N. Pirzada, M. Y. Nayan, F. Subhan, M. F. Hassan, M. A. Khan, “Comparative analysis of active and passive indoor localization systems,” AASRI Procedia, vol. 5, pp. 92–97, 2013, doi: https://doi.org/10.1016/j.aasri.2013.10.063.
- B. Sulaiman, E. Natsheh, S. Tarapiah, “Towards a better indoor positioning system: A location estimation process using artificial neural networks based on a semi-interpolated database,” Pervasive Mob. Comput., vol. 81, p. 101548, 2022, doi: https://doi.org/10.1016/j.pmcj.2022.101548.
- H. Mehmood, N. K. Tripathi, T. Tipdecho, “Indoor positioning system using artificial neural network,” J. Comput. Sci., vol. 6, no. 10, pp. 1219–1225, 2010, doi: https://doi.org/10.3844/jcssp.2010.1219.1225.
- O. Lemeshko, J. Papan, M. Yevdokymenko, O. Yeremenko, “Advanced tensor solution to the problem of inter-domain routing with normalized quality of service,” Appl. Sci., vol. 12, no. 2, p. 846, 2022, doi: https://doi.org/10.3390/app12020846.
- O. Lemeshko, J. Papan, O. Yeremenko, M. Yevdokymenko, P. Segec, “Research and development of delay-sensitive routing tensor model in IoT core networks,” Sensors, vol. 21, no. 11, p. 3934, 2021, doi: https://doi.org/10.3390/s21113934.
- I. Strelkovskaya, I. Solovskaya, J. Strelkovska, “The use of linear complex planar splines to improve the accuracy of determining the location of the user in Wi-Fi/indoor networks,” in 2021 IEEE 8th International Conference on Problems of Infocommunications, Science and Technology (PIC S&T), 2021, pp. 613–616, doi: https://doi.org/10.1109/PICST54195.2021.9772175.
- I. Strelkovskaya, I. Solovskaya, J. Strelkovska, “Linear complex planar splines in Wi-Fi/indoor positioning problems,” in 2021 IEEE International Conference on Information and Telecommunication Technologies and Radio Electronics (UkrMiCo), 2021, pp. 84–87, doi: https://doi.org/10.1109/UkrMiCo52950.2021.9716612.
- I. Strelkovskaya, I. Solovskaya, J. Strelkovska, “Fingerprinting/indoor positioning using complex planar splines,” J. Electr. Eng., vol. 72, no. 6, pp. 401–406, 2021, doi: https://doi.org/10.2478/jee-2021-0057.
- I. Strelkovskaya, I. Solovskaya, J. Strelkovska, T. Grygoryeva, “Using quadratic complex planar splines in solving local positioning problems,” in 2022 IEEE 16th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), 2022, pp. 602–605, doi: https://doi.org/10.1109/TCSET55632.2022.9766876.
- V. I. Belyi, I. V. Strelkovskaya, “Approximation of functions by analytic complex splines in domains with quasiconformal boundary,” Ukr. Math. J., vol. 40, no. 5, pp. 481–486, 1989, doi: https://doi.org/10.1007/BF01057525.
- G. Opfer, M. L. Puri, “Complex planar splines,” J. Approx. Theory, vol. 31, no. 4, pp. 383–402, 1981, doi: https://doi.org/10.1016/0021-9045(81)90104-0.