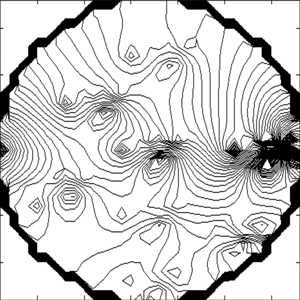
Visualization of surface conductivity distributions of tomography cross-section using conductivity zones method
DOI:
https://doi.org/10.3103/S0735272713070078Keywords:
electrical impedance tomography, EIT, conductivity zones, modification method, regularization, matrix conditionality, forward problem, inverse problem, finite elements method, phantomAbstract
Conductivity zones method is suggested that allows reconstructing the image of electrical impedance tomography with essentially lower computation expenses. Results of reconstruction performed by regularizing the matrix of contour-edge voltage derivatives with respect to zones’ surface conductivities.
References
- BROWN, B.H. AND BARBER, D.C. Electrical Impedance Tomography. Clin. Phys. Physiol. Meas., v.13, Sappl. A, 1992.
- WEBB, S. (ed.), The Physics of Medical Imaging. Taylor & Francis, 1988.
- PEKKER, YA.S.; BRAZOVSKIY, K.S.; USOV, V.YU.; PLOTNIKOV, М.P.; UMANSKIY, О.S. Electrical Impedance Tomography. Tomsk: NTL, 2004. 190 p. [in Russian].
- RYBIN, А.I.; MOVCHANIUK, А.V.; LUGOVSKIY, А.F. Application of electrical impedance tomography in mechatronic systems with ultrasound cavitators. Visnyk NTUU KPI. Ser. Mashynobuduvannya, n.64, p.67-75, 2012.
- SUSHKO, I.А.; GAIDAYENKO, YE.V.; MOVCHANIUK, А.V.; RYBIN, А.I. Estimation of cavitation level using electrical impedance tomography. Visnyk NTUU KPI. Ser. Radiotekhnika. Radioaparatobuduvannya, n.48, p.168-178, 2012.
- METHERALL, P.; BARBER, D.C.; SMALLWOOD, R.H.; BROWN, B.H. Three-dimensional electrical impedance tomography. Nature, v.380, p.509-512, Apr. 1996. doi: http://dx.doi.org/10.1038/380509a0">10.1038/380509a0.
- BAHRANI, NAVID, 2½D finite element method for electrical impedance tomography considering the complete electrode model. Ph.D. thesis. Department of Systems and Computer Engineering Carleton University, Ottawa, 2012.
- CHENEY, M.; ISAACSON, D.; NEWELL, J.C. Electrical impedance tomography. SIAM Rev., v.41, n.1, p.85-101, 1999. PII: http://linkinghub.elsevier.com/retrieve/pii/S0036144598333613">S0036144598333613.
- SILVESTER, P.P. AND FERRARI, R.L. Finite Elements for Electrical Engineers. New York: Cambridge University Press, 1983. 229 p.
- KORZHENEVSKIY, А.V.; KUL’TISOV, YU.S.; CHEREPNIN, V.А. RU Patent No. 2127075, 1996.
- DOROZHOVETS’, М.; FEDORCHUK, А.; PETROVS’KA, І. Mathematical basics of direct problem of conductivity tomography. Visnyk NU Lvivska Politekhnika. Ser. Avtomatyka vymiryuvannya ta keruvannya, n.324, p.43-51, 1998.
- RYBINA, I.А. Solution of direct problem of electrical impedance tomography using methods of cuircuits theory. Visnyk NTUU KPI. Ser. Radiotekhnika. Radioaparatobuduvannya, n.43, p.4-13, 2010.
- SUSHKO, І.A. Algorithm for solving direct problem of electrical impedance tomography using modification method. Visnyk NTUU KPI. Ser. Radiotekhnika. Radioaparatobuduvannya, n.47, p.165-175, 2011.
- RYBIN, А.I. Numerical-symbolic analysis of electrical circuits using generalized method of modification. Pratsi Instytutu Elektrodynamiky NAN Ukrainy, IED NANU, n.1, p.28-30, 2002.
- RYBIN, А.I. Precision estimation of solving linear circuit analysis problem using modification method. Radioelectron. Commun. Syst., v.44, n.5, p.40, 2001.
- RYBINA, І.A.; RYBIN, A.І.; SHARPAN, О.B. Calculation of transfer impedance derivatives with respect to surface conductivity of edge elements when solving reverse problem of electrical impedance tomography. Visnyk NTUU KPI. Ser. Radiotekhnika. Radioaparatobuduvannya, n.44, p.5-11, 2011.
- VAUHKONEN, M.; VADASZ, D.; KARJALAINEN, P.A.; SOMERSALO, E.; KAIPIO, J.P. Tikhonov regularization and prior information in electrical impedance tomography. IEEE Trans. Med. Imaging, v.17, n.2, p.285-293, 1998. doi: http://dx.doi.org/10.1109/42.700740">10.1109/42.700740.
- SUSHKO, І.A.; GAYDAIENKO, YE.V.; YAKUBENKO, О.А. Potential sensitivity of electrical impedance tomography. Visnyk NTUU KPI. Ser. Radiotekhnika. Radioaparatobuduvannya, n.50, p.92-104, 2012.
- TIKHONOV, А.N. AND ARSENIN, V.YA. Methods of Solving Incorrect Problems. Moscow: Nauka, 1979. [in Russian].
Downloads
Published
2013-07-23
Issue
Section
Research Articles

